Discussion of Total Variation Minimization Norm for Image Denoising

Introduction: 
Image restoration, especially image denoising, is a very important process and is often necessary as a pre-processing for other imaging techniques such as segmentation and compression. For the last two decades, various partial differential equation (PDE) based models have been developed for this purpose [1, 5, 8, 9, 10, 11, 13, 14, 15, 17, 18, 19, 20]. In general, an observed image $f$, corrupted by Gaussian noise $n$, is represented by the equation $$f= u+n,$$ where $u$ is the original noise free image. Here $u,f: \Omega \subset R^2 -> R$. For any denoising model, the main objective is to reconstruct $u$ from an observed image $f$.
In 1992, Rudin, Osher, and Fatemi \cite{rudin_rof1992} proposed the total variation (TV) denoising model. In this article we see how this model was build up using PDE methods. The model was based on $L_1$ norm. We will first see how the $L_1$ norm is more effective in preserving the edges than $L_2$ norm and finally we will discuss how the TV model was developed using some constraints along with the $L_1$ minimization norm. Before we start the discussion let us have a look at a very elementary image

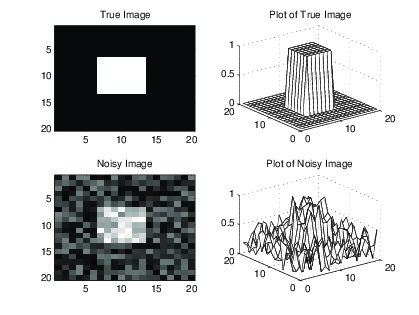From the image plot, we can see we have some sharp edges introduced by the noise in the clean image and we need to diffuse them to get back the original image. Hence we need to apply diffusion operator on the image function to remove the noise. 

$L_2$ norm in image denoising:  
As we have seen, noise denoising is primarily associated with diffusion and hence initially $L_2$ norm was used for this purpose. In this section we will discuss a denoising model built up on $L_2$ minimization norm. We will first build the model in both one and two dimensions and then see the effect of it.
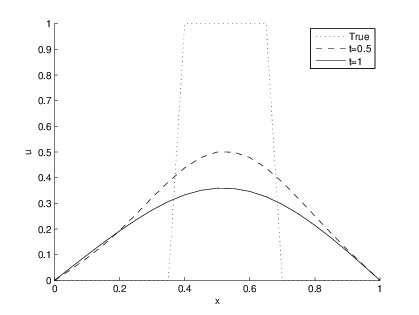
$L_2$ norm on 1 dimension -  $L_2$ norm functional in 1-dimension is given by $$F=\int|u_x|^2 dx$$Since we want to diffuse the noise, we are interested in minimizing the above functional. For that we find the equivalent Euler- Lagrange equation. This is given by $0=u_{xx}$ and using the time-marching scheme we get the system as $$u_t=u_{xx}$$ This is our $L_2$ norm model for $1$-dimension. Below are the results:

$L_2$ norm on 2 dimension - Now we build up the $L_2$ norm model for $2$-dimensions. $L_2$ norm functional in 2-dimensions is given by $$F=\int\left|\nabla u\right|^2 dx dy = \int\left(u_x^2+u_y^2\right)dxdy$$ The Euler- Lagrange equation is given by $$0=u_{xx}+u_{yy}$$ Using the time-marching scheme we get the system as $$u_t=u_{xx}+u_{yy}$$ and below we have the results:
                            
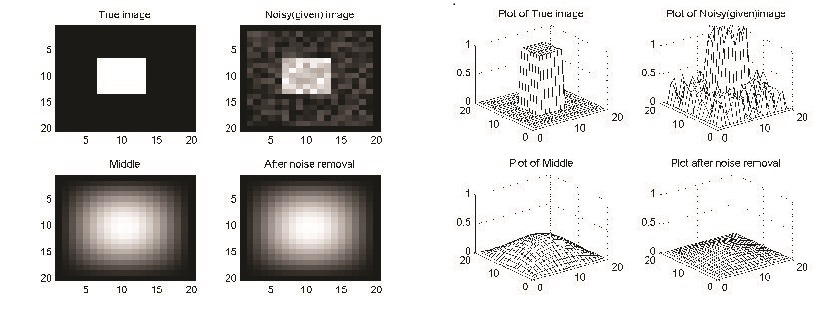
Hence it is obvious from the results that $L_2$ norm is not efficient for diffusion. It diffuses the edges of the original image along with the noise.
 
$L_1$ norm in image denoising:
Now we will discuss a denoising model built up on $L_1$ minimization norm. As before, we will first build the model in both one and two dimensions and then see the effect of it.
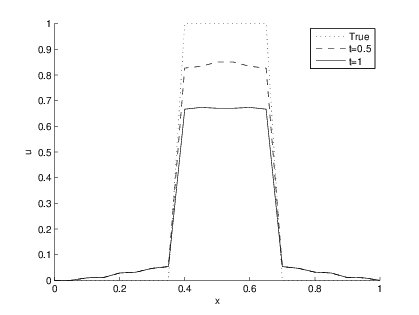
$L_1$ norm on 1 dimension - $L_1$ norm functional in 1-dimension is given by $$F=\int\left|u_x\right|dx$$ The Euler-Lagrange equation is given by $$0=\frac{\partial}{\partial x}\left(\frac{u_x}{\left|u_x\right|}\right)$$ Using the time-marching scheme we get the model as $$u_t=\frac{\partial}{\partial x}\left(\frac{u_x}{\left|u_x\right|}\right)$$ Below is the result for this model:

$L_1$ norm on 2 dimension -  $L_1$ norm functional in $2$-dimension is given by $$F=\int\left|\nabla u\right|dxdy=\int\sqrt{u_x^2+u_y^2}dxdy$$ The Euler-Lagrange equation is given by $$0=\frac{\partial}{\partial x}\left(\frac{u_x}{\sqrt{u_x^2+u_y^2}}\right)+\frac{\partial}{\partial y}\left(\frac{u_y}{\sqrt{u_x^2+u_y^2}}\right)$$ Using the time-marching scheme we get the system as $$u_t=\frac{\partial}{\partial x}\left(\frac{u_x}{\sqrt{u_x^2+u_y^2}}\right)+\frac{\partial}{\partial y}\left(\frac{u_y}{\sqrt{u_x^2+u_y^2}}\right)$$

Now we see the results of the $2$-dimensional image which is shown below.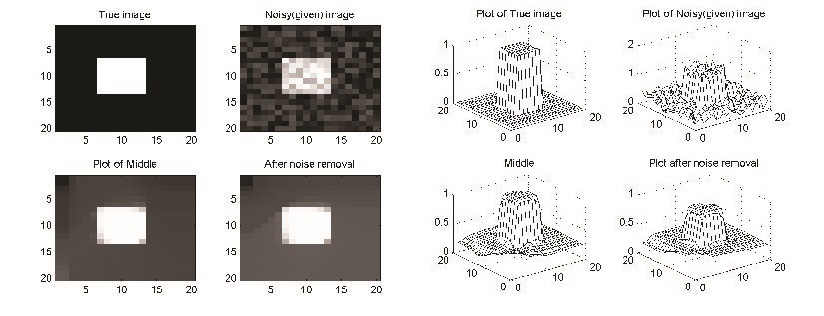

We can see $L_1$ norm has much better edge preserving properties than $L_2$ norm.

Total variation minimization norm:
From the previous sections we can see essentially both $L_1$ and $L_2$ norm gives us diffusion of the original image. But we want to diffuse only the noise not the image itself. To rectify this, Rudin, Osher, and Fatemi \cite{rudin_rof1992} proposed the total variation (TV) denoising model as the minimization problem: $$\min_u \int_\Omega\left|\nabla u\right|d\vec{x}$$

subject to the constraints, $$\int_{\Omega} f d\vec{x}  =\int_{\Omega} u d\vec{x}$$ and  $$\int_{\Omega}\frac{1}{2} \left(f-u\right)^2 d\vec{x}  =\sigma^2,$$ where $\sigma$ is the standard deviation of the noise $n$.
These constraints ensure that the resulting image and the observed images are close to each other. Combining the above constraints, the TV functional is obtained by: $$F(u) = \int_\Omega \left|\nabla u\right| d\vec{x} +\frac{\lambda}{2} \int_\Omega \left(f-u\right)^2 d\vec{x}.$$ Here, $\lambda$ is a constraint parameter. The equivalent Euler-Lagrange equation gives the TV denoising model as $$\frac{\partial u}{\partial t} - \nabla \cdot \left(\frac{\nabla u}{|\nabla u|}\right)=\lambda(f-u).$$ To avoid singularities, it was regularized by using $|\nabla u| \approx |\nabla u| = (u_x^2+u_y^2+\epsilon^2)^{1/2}$. Comparing TV norm with $L_1$ norm equations we see an extra fitting term, $-\lambda\left(u-u_0\right)$, is used with the $L_1$ norm. We try to see the effects of the fitting term on $L_2$ norm first.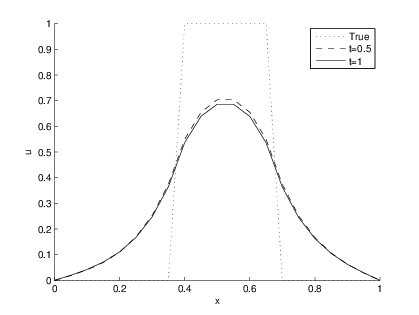

The $L_2$ norm gives better result with the fitting term. But it still diffuses the edges. We now look for results of TV norm which is same as the $L_1$ norm effects along with the fitting term.

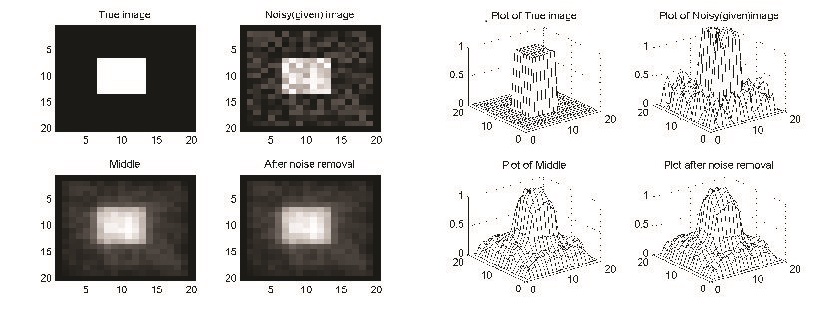
Obviously this preserves the original edges much better than both $L_1$ and $L_2$ norm. Below we have the results of TV norm on a real image as we can see below.
Conclusion:
In this article we discussed how we can have efficient denoising using the PDE based ROF model. It gives us much better results than simple denoising techniques such as linear smoothing. But one of the biggest drawbacks of the TV model is that it introduces some staircasing effect in the denoised image. Later some more PDE based models were developed to improve this feature [6, 7, 8, 13, 14, 20]. Also, there were some filtering based models which was very effective in removing the staircasing effects [2, 3, 4, 12, 16]. But still the ROF model is considered to be an important milestone in image denoising methods.

References:
[1] Luis Alvarez, Pierre-Louis Lions, and Jean-Michel Morel. Image selective smoothing and edge detection by nonlinear diffusion. ii. SIAM J. Numer. Anal., 29(3):845–866, June 1992.
[2] A. Buades, B. Coll, and J.-M. Morel. A non-local algorithm for image denoising. In Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on, volume 2, pages 60 – 65 vol. 2, june 2005.
[3] Antoni Buades, Bartomeu Coll, and JeanMichelMorel. On image denoising methods. Technical report, Technical Note, CMLA (Centre de Mathema- tiques et de Leurs Applications, 2004.
[4] Antoni Buades, Bartomeu Coll, and Jean-Michel Morel. Neighborhood filters and pde’s. Numer. Math., 105:1–34, October 2006.
[5] Francine Catt´e, Pierre-Louis Lions, Jean-Michel Morel, and Tomeu Coll. Image selective smoothing and edge detection by nonlinear diffusion. SIAM J. Numer. Anal., 29(1):182–193, February 1992.
[6] Youngjoon Cha and Seongjai Kim. Monte: The method of nonflat time evolution in pde-based image restoration, 2005.
[7] Tony Chan, Antonio Marquina, and Pep Mulet. High-order total variation-based image restoration. SIAM Journal on Scientific Computing, 22(2):503–516, 2000.
[8] Tony Chan and Luminita Vese. Variational image restoration and segmentation models and approximations. UCLA CAM Report 47, October 1997.
[9] Tony F. Chan, Gene H. Golub, and Pep Mulet. A nonlinear primal-dual method for total variation-based image restoration. SIAM J. Sci. Comput., 20:1964–1977, May 1999.
[10] Kisee Joo and Seongjai Kim. Pde-based image restoration, i: Anti-staircasing and anti-diffusion. Image Rochester NY, pages 1–19, 2003.
[11] Kisee Joo and Seongjai Kim. Pde-based image restoration, ii: Numerical schemes and color image denoising. Technical report, University of Kentucky, 2003.
[12] Venkateswarlu Karnati, Mithun Uliyar, and Sumit Dey. Fast non-local algorithm for image denoising. 2009 16th IEEE International Conference on Image Processing ICIP, 6812(0):3873–3876, 2009.
[13] Seongjai Kim. Loss and recovery of fine structures in pde-based image denoising. In Proceedings of the Fifth Conference on Mathematics and Image Analysis, Paris France, September 6-9 2004.
[14] Seongjai Kim and Hyeona Lim. A non-convex diffusion model for simultaneous image denoising and edge enhancement. Electronic Journal of Differential Equations, Conference 15:175–192, 2007.
[15] Pierre Kornprobst, Rachid Deriche, and Gilles Aubert. Nonlinear operators in image restoration. In In Proceedings of the International Conference on Computer Vision and Pattern Recognition, pages 325–331. IEEE Computer
Society, IEEE, 1997.
[16] Mona Mahmoudi and Guillermo Sapiro. Fast image and video denoising via nonlocal means of similar neighborhoods. IEEE Signal Processing Letters, 12:839–842, 2005.
[17] Antonio Marquina and Stanley Osher. Explicit algorithms for a new time dependent model based on level set motion for nonlinear deblurring and noise removal. SIAM J. Sci. Comput, 22:387–405, 1999.
[18] Pietro Perona and Jitendra Malik. Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12:629–639, 1990.
[19] Leonid I. Rudin, Stanley Osher, and Emad Fatemi. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena, 60(1-4):259 – 268, 1992.
[20] Luminita Vese and Tony F. Chan. Reduced non-convex functional approximations for image restoration & segmentation. UCLA CAM Report 56, 1997.

About the Author
Dr. Arundhati Bagchi Misra is an Assistant Professor of Mathematics at Saginaw Valley State University, Michigan, USA. She has obtained her Bachelors and Masters degree in Mathematics from University of Kalyani and her Phd. in Mathematics from Mississippi State University. Her research interest focusses on numerical analysis and image denoising.