Bitcoins are digital coins which are not issued by any government, bank, or organization, and rely on cryptographic protocols and a distributed network of users to mint, store, and transfer. The scheme was ?rst suggested in 2008 by Satoshi Nakamoto, and became fully operational in January 2009. It had attracted a large number of users and a lot of media attention. How much is a bitcoin worth? Well, it’s worth whatever somebody will pay for a unit of the online currency, which as I write this is 626.93 US Dollar, up by 100 times from 6.65 US Dollar two years ago. How does one mint a bitcoin? What is the maths behind it? Is it robust? We will answer some of these questions in this article.
Lets start with reflecting little bit on why is first place one need Bitcoins? For that we start with the concept of money. Money is a container for deferred payment, a promised value, and it is a verifiable record. A government, bank, or organization works as an authority to ensure verifiability and providing promised value. For deferred payment e.g. settling a debt, government or international treaty can be in enforcement.
The premise of Bitcoin is ever increasing volume of transaction over digital communication channel, where ensuring the definition of money is in the hand of financial institutes. This is a third party trust based model. It is rather unlikely, that you have never faced the problem inherent in such system - where money was deducted from your account, but payment was not received in exchange (of goods that have purchased). As volume of transaction over digital communication channel increases, fraud, failure and dispute volume will increase. As per Nilson Report the global card fraud amounts to $11.27 billion in calendar year 2012. Reversal of the transaction becomes unavoidable because of failure, and in the presence of fraud - trust becomes distributed (institute must trust you to perform reversal).
If two willing parties can transact directly with each other without the need for a trusted third party, then that would be a cost effective solution - as maintaining distributed trust in the face of increased, fraud, failure and dispute is an ever growing cost. So how can you get some bitcoin? After all it's just a string of 0 and 1, so why to hack it up? Well for a money (genuine or a fake one) to work it must be acceptable by another party, and for a digital money like Bitcoin what can be better than double spend it (use the same money to transact many times). To be able to do this we must start with transaction process with a Bitcoin before we can hack one up.
Recall that a function is defined by two sets $X$ and $Y$ and a rule $f$ which assigns to each element in $X$ one element in $Y$. The image $y$ of $x$ is denoted by $y = f(x)$. Preimage of $y$ is an element $x \in X$ for which $f(x) = y$. The set of all elements in $Y$ which have at least one pre-image is called the image of $f$, denoted $Im(f)$. A function $f$ from a set $X$ to a set $Y$ is called a one-way function if $f(x)$ is “easy” to compute for all $x \in X$ but for “essentially all” elements $y \in Im(f)$ it is “computationally infeasible” to find any $x \in X$ such that $f(x) = y$. Let’s consider an example, select primes $p = 48611$, $q = 53993$, form $n = pq = 2624653723$, and let $X = {1, 2, 3, \ldots, n − 1}$. Define a function $f$ on $X$ by $f(x) = r_{x}$ for each $x \in X$, where $r_{x}$ is the remainder when $x^{3}$ is divided by $n$. For instance, $f(2489991) = 1981394214$ since $24899913 = 5881949859 · n + 1981394214$. Computing $f(x)$ is a relatively simple thing to do, but to reverse the procedure is much more difficult.
A trapdoor one-way function is a one-way function $f$ from a set $X$ to a set $Y$ with the additional property that given some extra information (called the trapdoor information) it becomes feasible to find for any given $y \in Im(f )$, an $x \in X$ such that $f(x) = y$.
One-way functions and trapdoor one-way functions play the defining role of cryptographic building blocks required for building the Bitcoin system. A cryptographic primitive which is fundamental in authentication, authorization, and non-repudiation is the digital signature. The purpose of a digital signature is to provide a means for an entity to bind its identity to a piece of information. The process of signing entails transforming the message and some secret information held by the entity into a tag called a signature.
A bitcoin can be thought of as a chain of transactions from one owner to the next. In the transaction owners are identified by their public key. In each transaction, the previous owner signs a hash of the transaction in which he received the bitcoins and the public key of the next owner - using the secret signing key corresponding to his public key. This signature (i.e., transaction) can then be added to the set of transactions that constitutes the bitcoin. Since each of these transactions refer the previous transaction (i.e., in sending bitcoins, the current owner must specify where they came from), the transactions form a chain. To verify the validity of a bitcoin, a user can check the validity of each of the signatures in this chain.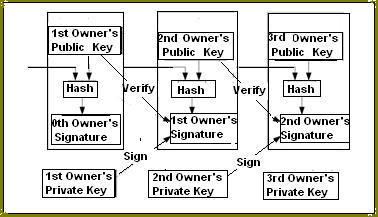
Transaction Chain in Bitcoin Formation
To prevent double spending, all users of the system is made aware of all transactions. Double spending can then be identified when a user attempts to transfer a bitcoin after he has already done so. To determine which transaction came first, transactions are grouped into blocks and time stamped to vouch for their validity. Time stamped Blocks are formed into a chain, with each block referencing the previous one (and thus further reinforcing the validity of all previous transactions). This process yields a block chain, which is then publicly available to every user within the system.
We must hack the time stamping system then to have our bitcoin accepted. Yes, block formation is the core of a valid bitcoin formation, and this is how bitcoins are generated in the first place. The figure illustrating the Bitcoin block formation is shown below. In fact, this happens in the process of forming a block: each accepted block (i.e., each block incorporated into the block chain) is required to be such that, when all the data inside the block is hashed, the hash begins with a certain number of zeroes. Time stamping / block formation mechanism here works based on proof-of-work system. A proof of work is a piece of data which is costly, and time-consuming to produce so as to satisfy certain requirements (e.g. produce a hash using SHA256 which has 52 leading zeros). It must be trivial to check whether data satisfies said requirements (that a hash has 52 leading zeros), while producing a valid proof of work involves a lot of trial and computation on average.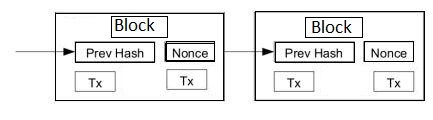
However we are in a decentralized system and we have no central authority producing bitcoin blocks. To allow users to find this particular collection of data, blocks contain, in addition to a list of transactions, a nonce. Once someone finds a nonce that allows the block to have the correctly formatted hash, the block is then broadcast in the same peer-to-peer manner as transactions. To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they're generated too fast, the difficulty increases. The system is designed to generate only 21 million bitcoins in total. Finding a block currently comes with an attached reward of 25 BTC; this rate was 50 BTC until November 28 2012 (block height 210,000), and is expected to halve again in 2016, and eventually drop to 0 in 2140.
About the Author
Subhas Kumar Ghosh (email: subhas.k.ghosh@gmail.com) received his bachelor degree in Electrical Engineering from Indian Institute of Technology, Kharagpur, India. His interests include computer security, graph theory, distributed computing, and approximation algorithms. His current interests also includes text analysis, and machine learning. Subhas has 25 international journal and conference publication. Over 19 years Subhas has worked with many corporate research labs including Honeywell Labs and Siemens Corporate Technology. Recently he has co-founded a text analysis start-up, and works as a consultant for a silicon valley based big-data start-up.