We will start this topic with the statement of Fundamental Theorem of Arithmetic.
Fundamental Theorem of Arithmetic: Every positive integer $n > 1$ can be expressed as a product of primes; and this representation is unique apart from the order in which the factors occur.
By collecting like primes and replacing them by a single factor, the above theorem can be rephrased more formally as follows.
Any positive integer $n > 1$ can be written uniquely as $$n = p_{1}^{k_1}.p_{2}^{k_2}\ldots.p_{t}^{k_t},$$ where each $p_{i}$ for $i = 1, 2, \ldots, t$ is a prime along with the property that $p_{i} \neq p_{j}$ for $i \neq j$ and each $k_{i} > 0$ for $i = 1, 2, \ldots, t$.
Given a positive integer $n,$ let $c(n)$ denote the number of positive divisors of $n$. If $n = p_{1}^{k_1}.p_{2}^{k_2}\ldots.p_{t}^{k_t}$ is the prime factorization of $n,$ then $$c(n) = (k_{1} + 1)(k_{2} + 1)\ldots(k_{t} + 1).$$For example, if $n = 180 = 2^{2}.3^{2}.5$, then $n$ has $c(n) = (2 + 1).(2 + 1).(1 + 1) = 18$ positive divisors. And these divisors are $1, 2, , 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180.$
We will now look into a few interesting problems invloving $c(n)$. The problems have been chosen from http://math2.uncc.edu/~hbreiter/TeachersCircle/Divisors.pdf.
Problem 1: Find the number of three digit divisors of $3600$.
Solution: $3600 = 2^{4}.3^{2}.5^{2}$ and hence $3600$ has $5.3.3 = 45$ divisors including $1$ and $3600.$
Note that $36 = 2^{2}.3^{2}$ has 9 divisors and they are $1, 2, 3, 4, 6, 9. 12, 18, 36$
Similarly, $100 = 2^{2}.5^{2}$ also has 9 divisors and they are $1, 2, 4, 5, 10, 20, 25, 50, 100.$
Note that, first two divisors of $100$, i.e, $1,2$ when will be multiplied with any divisors of $36$ will not yield a divisors of $3600$ which is of three digit.
For the divisors $4, 5$ of $100$ the only divisor of $36$ is the number itself which on multiplying gives rise a three digit divisor of $3600$, viz $A = \{144, 180\}.$
The divisor $10$ of $100$ on multiplting with the divisors $12, 18, 36$ of $36$ produces $B = \{120, 180, 360\}.$
The divisor $20$ of $100$ on multiplting with the divisors $6, 9, 12, 18, 36$ of $36$ produces $C = \{120, 180, 240, 360, 720\}.$
The divisor $25$ of $100$ on multiplting with the divisors $4, 6, 9, 12, 18, 36$ of $36$ produces $D = \{100, 150, 225, 300, 450, 900\}.$
The divisor $50$ of $100$ on multiplting with the divisors $2, 3, 4, 6, 9, 12, 18$ of $36$ produces $E = \{100, 150, 200, 300, 450, 600, 900\}.$
The divisor $100$ of $100$ on multiplting with the divisors $1, 2, 3, 4, 6, 9$ of $36$ produces $F = \{100, 200, 300, 400, 600, 900\}.$
Therefore, $A \cup B \cup C \cup \ldots \cup F = \{100, 120, 144, 150, 180, 200, 225, 240, 300, 360, 400, 450, 600, 720, 900\}$. Hence, the number of three digit divisors of $3600$ is $15$.
Problem 2: How many of the positive integer divisors of $N = 2^{3}.3^{3}.5^{3}.7^{3}.11^{3}$ have exactly $12$ positive integer divisors.
Solution: Note that, $12$ can be expressed in any of the following ways. (i) $12 = (2 + 1)(3 + 1)$, (ii) $12 = (2 + 1)(1 + 1)(1 + 1)$ , (iii) $12 = (1 + 1)(5 + 1)$.
So, a divisor of $N$ will be having $12$ positive integer divisors if the divisor itself can be written in any of the following forms - (i) $p_{1}^{2}.p_{2}^{3}$, (ii) $p_{1}^{2}.p_{2}.p_{3}$ and (iii) $p_{1}^{2}.p_{2}^{5}$, where $p_{i}$'s $i = 1, 2, 3$ are primes.
Since we are talking about divisors of $N$ and $N$ in its prime factor decomposition does not have any prime with power greater than equal to $4$, so it can be easily concluded that $N$ will not have any divisor of the form $p_{1}^{2}.p_{2}^{5}$.
We first try to figure out divisors of $N$ of the form $p_{1}^{2}.p_{2}^{3}$. $p_{1}$ and $p_{2}$ both will be any of the primes from the set $\{2, 3, 5, 7, 11\}$ and since their($p_1$ and $p_2$) powers are equal, so there will be $5_{P_{2}} = 20$ such divisors of the form $p_{1}^{2}.p_{2}^{3}$.
We will now try to figure out divisors of $N$ of the form $p_{1}^{2}.p_{2}.p_{3}$. Note that there are $5$ options to choose $p_{1}$ from. After having fixed $p_{1}$, $p_{2}$ and $p_{3}$ will have to be chosen from a set with $4$ primes. Since the powers of $p_{2}$ and $p_{3}$ are equal, so there are $4_{C_{2}} = 6$ ways we can choose $p_{2}$ and $p_{3}$. Hence, $5 x 6 = 30$ divisors of $N$ exist of the form $p_{1}^{2}.p_{2}^{3}$.
So, $N$ has $30 + 20 = 50$ positive integer divisors with exactly $12$ positive integer divisors.
Problem 3: Let, $N = 69^{5} + 5.69^{4} + 10.69^{3} + 10.69^{2} + 5.69 + 1$. How many positive integers are factors of $N$.
Solution: Note that $N = 69^{5} + 5.69^{4} + 10.69^{3} + 10.69^{2} + 5.69 + 1 = (69 + 1)^{5} = 70^{5} = 2^{5}.5^{5}.7^{5}$.
Therefore, the number of positive factors of $N = 6.6.6 = 216$.
Problem 4: How many ordered pairs $(x, y)$ of positive integers satisfy $xy + x + y = 199$.
Solution: Note that, $xy + x + y + 1 = 200$ which implies $(x + 1)(y + 1) = 2^{3}.5^{2}$.
There are $(3 + 1)(2 + 1) = 12$ divisors of $200,$ viz, $1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200$. So, $x + 1$ and $y + 1$ both will assume values from the above set of divisors. Since, we are seeking solutions of $(x, y)$ where $x > 0$ and $y > 0$, so $x + 1$ can not be equal to $1$ and also $x + 1$ can not be equal to $200$, since in which case $y = 0$.
Therefore, $$(x, y) = (1, 99)$$$$(x,y) = (3, 49)$$$$(x,y) = (4, 39)$$$$(x,y) = (7, 24)$$$$(x,y) = (9, 19)$$$$(x,y) = (19, 9)$$$$(x,y)=(24,7)$$$$(x,y) = (39,4)$$$$(x,y) = (49,3)$$$$(x,y) = (99,1)$$
So, there are $10$ ordered pairs solving the relation $xy + x + y = 199$.
Problem 5: Find the number of odd divisors of $13!$.
Solution: $13! = 13.12.11.10.9.8.7.6.5.4.3.2.1 = (13.11.7.5^{2}.3^{5}).(2^2.2.2^{3}.2.2^{2}.2) = (13.11.7.5^{2}.3^{5}).(2^{10})$
So, number of odd divisors of $13!$ is equal to the number of divisors of $N = 13.11.7.5^{2}.3^{5}$ and which is equal to $2.2.2.3.6 = 144$.
Problem 6: Find the product $P$ of all divisors of $6^{3}$ and express your answer in the form of $6^{t}$, for some integer $t$.
Solution: $N = 6^{3} = 2^{3}.3^{3}$ and hence $N$ has $4.4 = 16$ divisors. In these set of $16$ divisors, each power of $2$ (i.e, $0, 1, 2, 3$) pairs with every power of $3$ (i.e, $0, 1, 2, 3$) as can be seen from the table below.
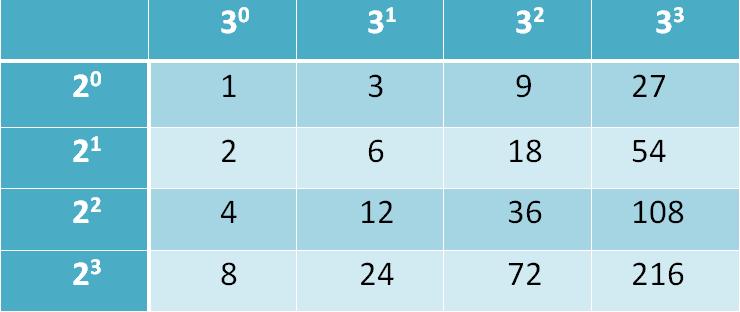
Each entry in the above matrix is a divisor and each row contributes $3^{6}$ when all the divisors in a row are multiplied. Denoting $P_{i}$ as the product of the divisors in a row, we can write $P_{i}$ as $P_{i} = (2^{i})^{4}.3^{6}
= 2^{4i}.3^{6}$ for $i = 0, 1, 2, 3$.
Therefore, $P = P_{0}.P_{1}.P_{2}.P_{3} = (3^{6}).(2^{4}.3^{6}).(2^{8}.3^{6}).(2^{12}.3^{6}) = 6^{24}$
Problem 7: The product of four distinct positive integers $a$, $b$, $c$ and $d$ is $8!$. The numbers also satisfy $$ab + a + b = 391$$$$bc + b + c = 199$$. What is $d!$.
Solution: From $ab + a + b = 391$ we have, $$(a + 1)(b + 1) = 392 = 2^{3}.7^{2}$$Hence, $a + 1$ and $b + 1$ will both assume values from the set $\{1, 2, 4, 7, 8, 14, 28, 49, 56, 98, 196, 392\}.$
From $bc + b + c = 199$ we have, $$(b + 1)(c + 1) = 200 = 2^{3}.5^{2}$$Hence, $b + 1$ and $c + 1$ will both assume values from the set $\{1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200\}.$
Therefore, $b + 1$ will assume values from the intersection of the above two sets of divisors and that is $\{1, 2, 4, 8\}$. Since, $b$ is a positive integer so $b + 1 \neq 1$ and hence $b$ is either $1$, $3$ or $7$.
If $b = 1$, then $a = 195 = 3.5.13$ and $c = 99 = 3^{2}.11$
If $b = 3$, then $a = 97$ and $c = 49 = 7^{2}$
If $b = 7$, then $a = 48$ and $c = 24$
Since $a.b.c.d = 8!$, so it is easy to see that $b$ can not be $1$ or $3$. Therefore, $b = 7$, $a = 48$ and $c = 24$. Putting the values of $a$, $b$ and $c$ in the relation $a.b.c.d = 8!$, it is easy to see that $d = 5$.