Definition
For any positive integer $n (>0)$ the factorial of $n$, denoted as $n!$, is defined as
\begin{align}
n! = n.(n-1).(n-2)\ldots.2.1. \hspace{2.2in} [1]
\end{align}
$0!$ is defined as $1$, i.e., $0! = 1,$ though it looks bit unintutive. From the definition, it is clear that
\begin{align}
n! = n.(n-1)! \hspace{3.5in} [2]
\end{align}
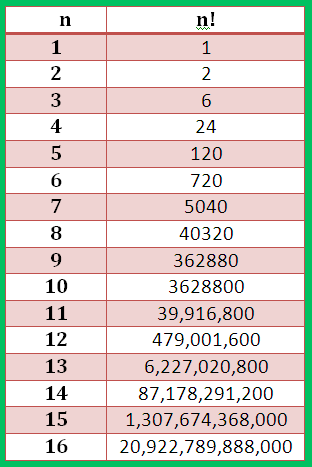
Now, for $n = 1$, we have $1! = 1.0!$ and this implies that $0! = 1$. So, now we see that the definition of $0!$ is in accordance with the equation (2). The figure below shows the values of the factorial for the integers $1$ to $16$ and we can see the valus of the factorial are getting bigger quickly as $n$ grows from $1$ to $16$. Also note that, for $n > 4$ each factorail ends with one or more $0$'s at the end.
Let us now take a look at, $$24! = 620,448,401,733,239,439,360,000$$ and $$25! = 15,511,210,043,330,985,984,000,000$$ We are now surprised to have seen $6$ trailing zeros instead of $5$ in $25!$. What went wrong?
The number $5$ when multiplied by any even number contributes a trailing zero at the end of the factorial. Up to $4!$, no number is divisible by $5,$ so there is no trailing zero.
(1) From $5!$ to $9!$, there is only one number,i.e. $5$ which is divisible by $5$, so there is only one trailing zero.
(2) From $10!$ to $14!$, there are two numbers $5$ and $10$ which are divisible by $5$, so there are $2$ trailing zeros.
(3) From $15!$ to $19!$, there are three numbers $5$, $10$ and $15$ which are divisible by $5$, so there are $3$ trailing zeros.
(4) From $20!$ to $24!$, there are four numbers $5$, $10$, $15$ and $20$ which are divisible by $5$, so there are $4$ trailing zeros.
In $25!,$ there are $5$ numbers $5$, $10$, $15$, $20$ and $25$ that are divisible by $5,$ but the number $25$ itself contributes one additional $5$ as a factor. This additional factor will also contribute one more trailing zero. That is why $25!$ has $6$ trailing zeros.
$n!$ when will be expressed as products of powers of primes will take the form
\begin{align}
\label{eq:3}
n! = 2^{c_1}.5^{c_2}.p_{1}^{c_3}.p_{2}^{c_4}.p_{3}^{c_5}\ldots, \hspace{3in} [3]
\end{align}
where $p_{i}$ ($i = 1,2,3,\ldots$) are primes other than $2$ and $5$ and $c_{i}$'s for $i = 1, 2, 3, \ldots$ are constants greater than $0$.
In $n!$, there are $\lfloor \frac{n}{2} \rfloor$ number of integers which are even and there are $\lfloor \frac{n}{5} \rfloor$ number of integers which are divisible by $5$ and $\lfloor \frac{n}{2} \rfloor > \lfloor \frac{n}{5} \rfloor.$ Also, if $m$ is the highest power of $5$ such that $k.5^{m} < n$ ($k > 0$), then $k.2^{m} < n$. In fact we have the following,
\begin{align}
\label{eq:4}
\lfloor \frac{n}{2^{j}} \rfloor > \lfloor \frac{n}{5^{j}} \rfloor \hspace{0.1in} for \hspace{0.1in} j = 1,2,\ldots,m \hspace{2.5in} [4]
\end{align}
and also
\begin{align}
\label{eq:5}
\lfloor\frac{n}{2^{j+1}} \rfloor > \lfloor \frac{n}{5^{j}}\rfloor \hspace{0.1in} for \hspace{0.1in} j = 1,2,\ldots,m \hspace{2.3in} [5]
\end{align}
\begin{align}
\label{eq:6}
=> \lfloor \frac{n}{2^{j}}\rfloor > 2.\lfloor \frac{n}{5^{j}}\rfloor \hspace{0.1in} for \hspace{0.1in} j = 1,2,\ldots,m \hspace{2.0in} [6]
\end{align}
Hence, for $j = 1, 2, \ldots, m,$ we have
\begin{align}
\label{eq:7}
\lfloor \frac{n}{2^{j}}\rfloor - \lfloor \frac{n}{2^{j+1}}\rfloor > \lfloor \frac{n}{5^{j}}\rfloor - \lfloor \frac{n}{5^{j+1}}\rfloor \hspace{2.5in} [7]
\end{align}
and also we have
\begin{align}
\label{eq:8}
\lfloor \frac{n}{2^{j}}\rfloor - \lfloor \frac{n}{2^{j+1}}\rfloor > \lfloor \frac{n}{5^{j}}\rfloor \hspace{3.0in} [8]
\end{align}
Denoting $\lfloor \frac{n}{5^{j}}\rfloor = c_{2j}$ for $j = 1, 2, \ldots, m$, $c_2$ can be expressed as,
\begin{align}
\label{eq:9}
c_2 = m.c_{2m} + (m-1).(c_{2(m-1)} - c_{2m}) + (m-2).(c_{2(m-2)} - c_{2(m-1)}) + \ldots + 2.(c_{22} - c_{23}) + (c_{21} - c_{22}) \hspace{0.5in} [9]
\end{align}
If $l$ is the highest power of $2$ such that $k^{'}.2^{l} < n$ ($k^{'} > 0$) and also ($l > m$), then $c_1$ can be written as,
\begin{align}
\label{eq:10}
c_1 = l.c_{1l} + (l-1).(c_{1(l-1)} - c_{1l}) + \ldots + m.(c_{1m} - c_{1(m+1)}) + \ldots + 2.(c_{12} - c_{13}) + (c_{11} - c_{12}) \hspace{1in} [10]
\end{align}
Because of the inequalities in relations (7) and (8), we see that for all $j = 1, 2, \ldots, m$, the coefficient of $j$ in equation (10) is greater than the coefficeint of $j$ in equation (9). Hence $c_{1} > c_{2}$ and this proves that each of the $5$'s in $5^{c_2}$ in equation (3) are capable of contributing to a trailing zero and the value of $c_2$ is computed following equation (9).
Corollary 1: If $n = 5^{k}$ and $k \geq 1$, then $n!$ has $\frac{5^k - 1}{4}$ trailing zeros.
Proof: Clearly, $m = k$ here, so following equation (9), we have $$c_2 = k.1 + (k-1).( \frac{5^k}{5^{(k-1)}} - 1) + (k-2).(\frac{5^k}{5^{(k-2)}} - \frac{5^k}{5^{(k-1)}}) + \ldots + (k - (k-1)).(\frac{5^k}{5^{(k-(k-1))}} - \frac{5^k}{5^{(k-(k-2))}})$$
\begin{align}
\label{eq:11}
=> c_2 = k + 4.5^0.(k-1) + 4.5^1.(k-2) + 4.5^2.(k-3)+\ldots+4.5^{k-2} \hspace{1.2in} [11]
\end{align}
\begin{align}
\label{eq:12}
=> \frac{c_2 - k}{4} = 5^0.(k-1) + 5^1.(k-2) + 5^2.(k-3)+\ldots+ 5^{k-2} = S (say) \hspace{0.9in} [12]
\end{align}
On simplification we get,
\begin{align}
\label{eq:13}
4.S = 5.S - S = (5 + 5^2 + 5^3 + \ldots + 5^{(k-1)}) - (k-1) \hspace{2.5in} [13]
\end{align}
\begin{align}
\label{eq:14}
\hspace{1.5in} c_{2} - k = \frac{5.(5^{k-1} - 1)}{4} - (k - 1) \hspace{2.8in} [14]
\end{align}
\begin{align}
\label{eq:15}
\hspace{2.0in} c_{2} = \frac{5^{k} - 1}{4} \hspace{3.8in} [15]
\end{align}
Corollary 2: If $n = c.5^{k}$, $k \geq 1$ and $c \in {2,3,4}$ then $n!$ has $c.\frac{5^k - 1}{4}$ trailing zeros.
Proof: Since $c \in {2,3,4}$, so the value of $m$ remains same for both $n$ and $\frac{n}{c}$.
Also note that each $c_{2j}$ for $n$ is $c$ times more than that of the $c_{2j}$'s for $\frac{n}{c}$ and the proof follows easily from this observation.
Problems
Prob1: How many zeros does $6250!$ end with?
Solution: We need to first find out highest power $m$ such that $k.5^{m} \leq = 6250$ for some $k > 0$. Note that, $2.5^{5} = 6250$ and hence $m = 5.$ Remember that, $c_{2j} = \lfloor \frac{n}{5^{j}} \rfloor$ for $j = 1, 2, \ldots, 5$. Therefore, $c_{25} = 2$, $c_{24} = 10$, $c_{23} = 50$, $c_{22} = 250$ and $c_{21} = 1250$. Hence, number of trailing zeros in $6250!$ is equal to $$c_{2} = 2.5 + (10 - 2).4 + (50 - 10).3 + (250 - 50).2 + (1250 - 250).1 == 1562$$
Prob2: If $n!$ has $20$ zeros at the end, then what are the possible values of $n$?
Solution: First we need to find out the lowest power $m_{1}$ such that $5^{m_{1}}!$ has more than $20$ trailing zeros, i.e., $c_2$ of $5^{m_{1}}! > 20$. From the corollary1 above, we can easily see that $5^{2}!$ has $6$ trailing zeros and $5^{3}!$ has $31$ trailing zeros.
Usng corollary 2, it can be concluded that $(3.5^{2})! = 75!$ has $18$ trailing zeros and $(4.5^{2})! = 100!$ has $24$ trailing zeros. So, the values of $n$ will be between $75$ and $100$.
Since $75!$ has $18$ trailing zeros, and we are required to find $n$ with $20$ trailing zeros. So, $2$ more $5$ factors we are required to add and this essentially means $75 + 2.5 = 85$ and hence $85!$ will have $20$ trailing zeros. The other possible values of $n$ are $86, 87, 88$ and $89$.