In September $1998$, Google went online and immediately after, it became clear that in comparison to other search engines Google delivered much relevant or high quality results up front. Founders of Google Sergey Brin and Larry Page, developed a ranking algorithm, called PageRank Algorithm, that exploits the link structure of the web to determine the importance of each page on the web. Google's PageRank algorithm has a high degree of influence on how the webpages are displayed in search for a query / keyword. Therefore, maximizing the PageRank score of a webpage with respect to a set of keywords has become an important component of company marketing strategies. In this article, we will briefly explain the concept and the mathematics behind the algorithm and it turns out to be a nice application of Linear Algebra.
PageRank algorithm works by modeling the behavior of a random web surfer who randomly selects links to navigate from one webpage to another. And this process continues until the web surfer decides to move to another webpage by some means other than selecting a link. Link structure of the web is represented as a directed graph, where the nodes of the graph are the webpages and are numbered as $1, 2, 3, \ldots, n$ and a directed arc from page $i$ to page $j$ is present, if there is a link from page $i$ to page $j$. PageRank algorithm quantifies the importance of a page by assigning score to each webpage. The score of page $k$ in the web is depicted as $x_{k} \geq 0$ (for $k = 1, 2, \ldots, n$). Zero score signifies a page with least possible significance. $x_{i} > x_{j}$ signifies that page $i$ is more important than page $j$.
The links to a given page are called backlinks for that page and more are the backlinks, the webpage is considered more important. This is because other webpages from which backlinks for a page originates considers the page t be important and therefore votes for the page
by linking to it. This is the central idea of assigning score to any webpage. But, considering the number of backlinks for a page as its score misses an important fact that a backlink from an important page (like AOL) should boost the score more than a backlink from a relatively unimportant page. To circumvent this problem PageRank algorithm implements a self-referential system where scre of a page $k$, i.e., $x_{k}$ is determined by the scores of all the pages $j (j \neq k)$, where page $k$ has a backlink from page $j$.
Having said all these let us now formalize all the discussions. The webpages are numbered from $1, 2, 3, \ldots, n$ and $x_{k}$ being the score of page $k$, for $k = 1, 2, \ldots, n$. The page $k$ contains $n_{k}$ links and these links point to some subset $L_{k}$ of $\{1, 2, \ldots, n\} - \{k\}$. Let, $B_{k}$ $\subset$ $\{1, 2, \ldots, n\} - \{k\}$ denote the set of pages with a link to page $k$, i.e., $B_{k}$ is the set of page $k$'s backlinks. For each page $k$, we then define the score $x_{k}$ as $$x_{k} = \sum\limits_{j \in B_{k}} \frac{x_{j}}{n_{j}} = \sum\limits_{j \in B_{k}} \frac{1}{n_{j}}.x_{j} + \sum\limits_{j \in B_{k}'} 0.x_{j}$$ where the sum has to be taken for all $j \in B_{k}$
Considering $a_{kj} = \frac{1}{n_{j}}$ for all $j \in B_{k}$ and $a_{kj} = 0$ for all $j \in B_{k}'$, the score $x_{k}$ of page $k$ for all $k = 1, 2, \ldots n$ can be written as $$x_{k} = (a_{k1}\hspace{0.2cm} a_{k2} \hspace{0.2cm} \ldots \hspace{0.2cm} a_{kn}) [x_{1} \hspace{0.2cm} x_{2}\hspace{0.2cm} \ldots \hspace{0.2cm} x_{n}]^T$$
Therefore,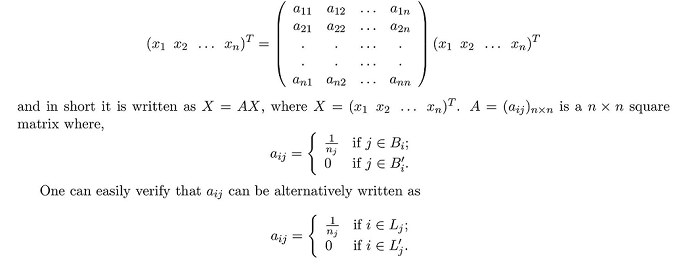
And this is valid since $i \in L_{j}$ implies $j \in B_{i}$ and vice versa. The matrix $A$ is called hyperlink matrix.
Therefore, finding the score for a page boils down to solving the system of linear equations $AX = X$ for $X$, where $X = (x_{1}\hspace{0.2cm}x_{2}\hspace{0.2cm} \ldots \hspace{0.2cm} x_{n})^T$ and the square matrix $A$ is known. Remember that, if a square matrix $A$ satisfies $AX = \lambda X$, for some $\lambda > 0$ and $\lambda \in R$ and $X \neq 0$, then $\lambda$ is called the eigen value of $A$ and $X$ is called the eigen vector corresponding to eigen value $\lambda$. Hence, web ranking problem is equivalent to finding out the eigen vector $X$ corresponding to the eigen value $1$ of the hyperlink matrix $A$.
References
[1] Kurt Bryan and Tanya Leise, The \$25,000,000,000 Eigenvector: The Linear Algebra Behind Google. In Journal SIAM Review, Volume 48, Issue 3, pages 569 - 581, 2006.
[2] Rebecca S. Wills, Google’s PageRank: The math behind the search engine. In Journal Math. Intelligencer, pages 6 - 10, 2006.